None of the images below are drawings but the results of rendering true 3D models.
Hover over ◊ for pop-up comments, and Greek letters for publishing details.
None of the images below are drawings but the results of rendering true 3D models.
Hover over ◊ for pop-up comments, and Greek letters for publishing details.
A full description of these .ttf files can be found on the separate fonts page, but they are included here as they are illusons in their own right, and can be downloaded via the links beneath each image. They are distributed under the Creative Commons Licence “BY-NC-ND” option.
The Romans were marvellous architects and engineers, as is shown by their aqueduct running from modern-day Uzès to Nîmes, which has a drop in height of 17m over its 50km length. However, I think even they would have had a bit of trouble constructing these.
The ivy in images 3b & 4b was created with Thomas Luft's free program, available here.






The textures here and above had already been made for use in The Pole Star Inn, so were not deliberately copied from the kind of brickwork featured in Jos de Mey's work.
















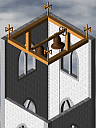
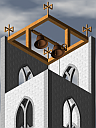


















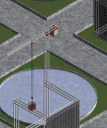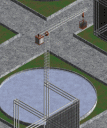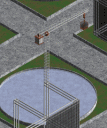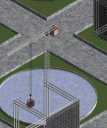












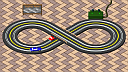




Motor #4 needs no batteries as it runs from the electricity created by its own internal generator, and Motor #5 removes the contra-rotating halves (required for Motor #2) to make a consistent impossible motor/generator, which then becomes a never-ending tower for Motor #6.
Both variations of this have a core that is perfectly possible in the real world, but rotating within an impossible framework.
Although similar to the mobius torus here, the orientation of this object is actually in two perpendicular axes as can be seen by the initial deconstruction.
Such objects are traditionally described as 'impossible' because they cannot be constructed as 3D objects or, when done so as on Oscar Reutersvärd's page, can only be seen from an isometric viewpoint due to overlapping elements. However, the simplest form of three cubes (cf. Opus 2B) can actually be constructed as a coherent object, as seen below in Tribars 4 & 5. The basis of this and all similar drawings/models involving cubes is that there are gaps between the cubes of approximately ½ width; however, due to the isometric viewpoint the arrangement is structurally identical to having the cubes physically touching one another with a ½-width offset. The following images (Tribars 3, 2, & 1) which are the classic triangle of cubes, are in its original form (cf. Opus 1 #293aa) completely impossible as each corner arrangement of three cubes is different to the minimalist "Opus 2B" and genuinely at 90°; however, by joining three of the smaller units it is possible to simulate an impossible object and only close examination reveals the cheat.